(1)多重分配。與單一分配相對,一個非跨境物流樞組結點可以發送或接受多個中心樞紐的物流。
(2)容量。關于容量有不同的說法。例如在一些相連結點或樞組上的容量,在該實驗室所作的研究里,“容量”總是指非中心結點從跨境物流樞紐收集的流量。我們用這種流量作研究起因于其在郵政上的首先應用。在郵政里,它取決于在樞紐中能被分類的郵件的數i的限制。
(3)中心跨境物流樞紐布局。與P個中心樞紐問題不同,這類問題不用于規定布局中的中心樞紐的數目。中心樞紐的數目通常取決于最小化成本,包括流量限制或運作中的中心物流樞紐的固定成本,或兩者同時考慮。
(4)物流臨界點。另一種變形,即物流經過一些或全部連接實現最小物流,但還未被廣泛研究。例如在很多航空公司可以根據流量臨界點,使用自己最小型號的飛機來防止網絡中出現不經濟的連接。
(三)USApHMP理論的基本模型
1.USApHMP—2下標公式
min二&EEW,(xD.Z + aDNZ:Zn + 6D,Z)
EZu=p
約束條件
2Zn=1,VEN
Zu≤Zk,
VikE N
ZkE10,1}
Vi.AE N
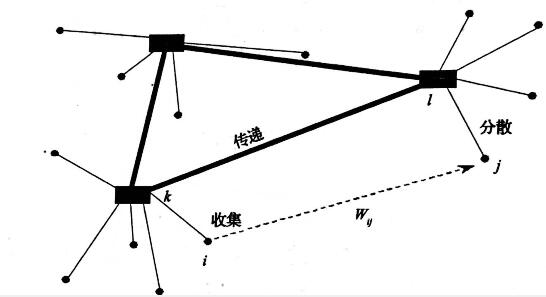
式中:,—結點i、j之間的客貨流量;Da,Du,D一分別為結點i與k、k與1、l與j之間的距離;x,a,6——分別為收集(Collection)成本系數、傳遞(Transfer)成本系數和分散(Distribution)成本系數;Zu,Z,—判斷流量是否存在的標準,其值為1表示有流量,值為0則無流量。
2.USApHMP4下標公式
&EEECwXu)
min(
2Zu=p
EZu=1
Vi,ke N
ZA≤Zu
Vi,hE N
Z.e{0,1}
Vi,h E N
2”yu =Zn
Vi,j,h E N
Eou =Z,
Vij,lE N
Xu≥0
Vi,ke N
Xu—通過跨境物流樞紐k、l的從結點i到j之間的流量存在開關,其和為1時表示有流量,為0時表示無流量;Cu—各段之間的成本系數;W,—結點i、j之間的流量。式也是建立在成本最低思想上,通過航段i、j之間的流量乘以其各段成本系數,得到各段成本,求和后得到其總成本。比較后確定最小的總運輸成本的方程所代表的布局為最終布局結構。
顯然,當P=N時,即每個結點都是中樞點時,中樞航線網絡又演化為若不考慮方向性,航班數量為N(N+1)/2。若考慮方向性,航班數量為N(N+1)。以后討論中我們均考慮方向性。如果有6個節點。顯然可以假定,各中樞點之間是相互連接的,而任一非中樞點可以與中樞點直接連接。


